Vous êtes-vous déjà demandé comment montrer que arctan(a) + arctan(b) = arctan((a+b)/(1-ab))? Si oui, vous êtes au bon endroit ! Nous allons plonger dans la formule des arctan, la démontrer et explorer ses applications pratiques. Attachez vos ceintures, car nous allons rendre les mathématiques du supérieur passionnantes et accessibles. Accrochez-vous, ça va être une balade arctangente !
Au sommaire :
- La formule arctan(a) + arctan(b) = arctan((a+b) / (1-ab)) est utilisée pour montrer la somme des tangentes inverses.
- L’arctan est la fonction inverse de la tangente et est généralement notée arctan x ou tan-1x.
- La formule de base pour déterminer la valeur de arctan est θ = tan-1(Perpendicular / Base).
- La démonstration de la formule arctan(a) + arctan(b) = arctan((a+b) / (1-ab)) dépend de la valeur de ab, si ab<1 ou ab>1.
- La formule arctan(x) ± arctan(y) = arctan[x ± y / 1 ± xy] est démontrée en utilisant la formule d’addition de la tangente.
- Il existe une formule bien connue pour arctan(a) + arctan(b) = arctan(a+b / 1-ab), jusqu’à un multiple de π.
Comprendre la formule des arctan
Avant de plonger dans la démonstration de la formule arctan(a) + arctan(b) = arctan((a+b) / (1-ab)), il est essentiel de comprendre ce que signifie arctan et comment il fonctionne dans le contexte trigonométrique. L’arctan, ou arc tangente, est la fonction inverse de la tangente. Dans le domaine de la trigonométrie, cela signifie qu’elle permet de retrouver l’angle dont la tangente est égale à un nombre donné. La formule de base pour déterminer la valeur de l’arctan est θ = tan-1(Perpendicular / Base).
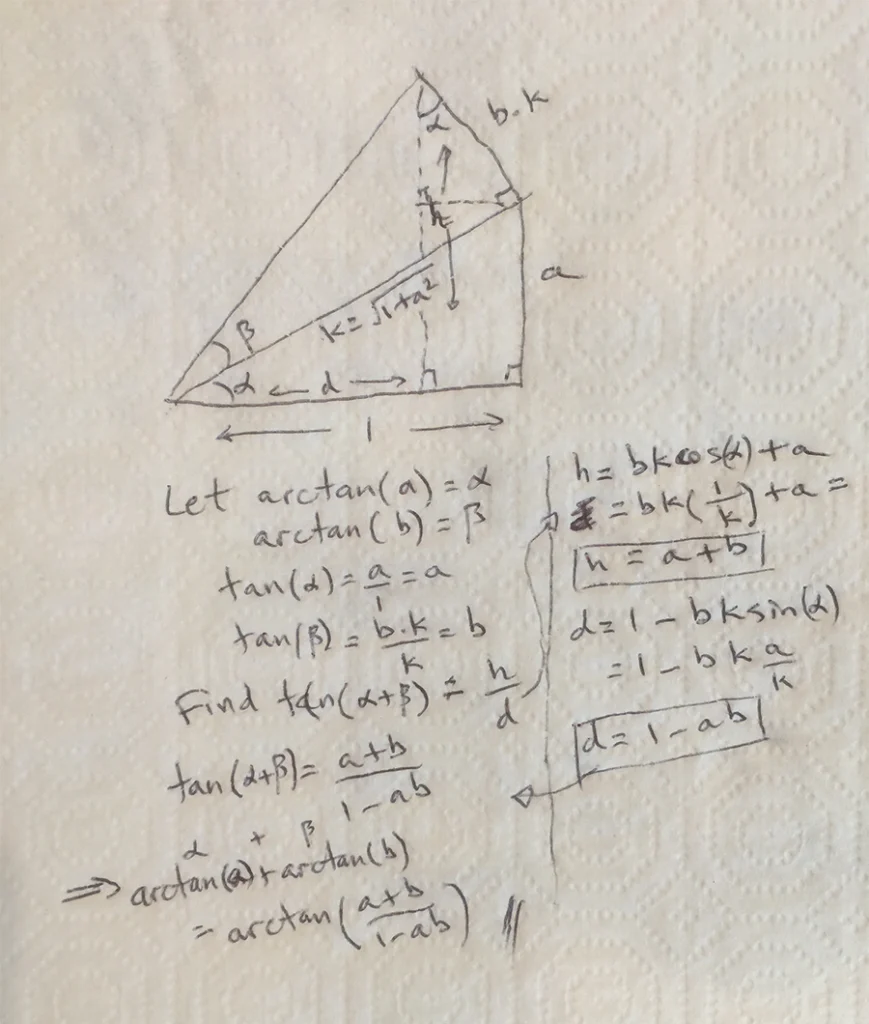
Cette formule est cruciale lorsque l’on travaille avec des angles et des triangles dans un plan cartésien. Elle est particulièrement utile dans des applications variées allant de la géométrie simple à des domaines plus complexes comme la navigation ou la robotique.
La formule arctan(a) + arctan(b) = arctan((a+b) / (1-ab)) est souvent utilisée pour trouver l’angle formé par la somme de deux autres angles dont les tangentes sont a et b. Cette formule est valide jusqu’à un multiple de π, sauf dans le cas où ab=1, où elle n’est pas définie.
Démonstration de la formule arctan
La démonstration de la formule peut être abordée en utilisant la formule d’addition de tangente. La formule de base de l’addition de tangentes est tan(α + β) = (tan α + tan β) / (1 – tan α tan β). En prenant l’arctangente des deux côtés de cette identité, on peut réarranger les termes pour obtenir l’identité recherchée.
Considérez α = arctan(a) et β = arctan(b). Alors, tan(α) = a et tan(β) = b. En substituant dans la formule d’addition, on obtient tan(α + β) = (a + b) / (1 – ab). En prenant l’arctan des deux côtés, on trouve α + β = arctan((a+b) / (1-ab)), ce qui prouve notre formule initiale.
Il est important de noter que cette équation tient compte du fait que les angles sont généralement considérés modulo π. Cela signifie que la formule est valide dans l’intervalle de -π/2 à π/2.
Applications pratiques et exemples
Comprendre et pouvoir démontrer cette formule a des implications pratiques importantes, notamment dans les domaines de l’ingénierie et de la physique. Par exemple, considérons le problème de trouver l’angle entre deux lignes dont les pentes sont connues. Si les pentes des lignes sont a et b, alors l’angle entre les lignes peut être trouvé en utilisant la formule des arctan.
Un autre exemple serait dans le domaine de la navigation, où la capacité de calculer précisément des angles est cruciale pour la direction et le positionnement corrects. La formule permet de combiner efficacement plusieurs mesures angulaires pour obtenir un résultat précis.
Ainsi, la formule arctan(a) + arctan(b) = arctan((a+b) / (1-ab)) n’est pas seulement un exercice de mathématiques théoriques, mais une composante essentielle à de nombreuses applications pratiques nécessitant une précision et une efficacité maximales dans le calcul des angles.
Qu’est-ce que l’arctan et comment fonctionne-t-il dans le contexte trigonométrique?
L’arctan, ou arc tangente, est la fonction inverse de la tangente. Dans le domaine de la trigonométrie, cela signifie qu’elle permet de retrouver l’angle dont la tangente est égale à un nombre donné. La formule de base pour déterminer la valeur de l’arctan est θ = tan-1(Perpendicular / Base).
Comment peut-on démontrer la formule arctan(a) + arctan(b) = arctan((a+b) / (1-ab))?
La démonstration de la formule peut être abordée en utilisant la formule d’addition de tangente. En prenant l’arctangente des deux côtés de cette identité, on peut réarranger les termes pour obtenir l’identité recherchée. En prenant l’arctan des deux côtés, on trouve α + β = arctan((a+b) / (1-ab)), ce qui prouve notre formule initiale.
Quelles sont les conditions de validité de la formule arctan(a) + arctan(b) = arctan((a+b) / (1-ab))?
La formule arctan(a) + arctan(b) = arctan((a+b) / (1-ab)) est valide jusqu’à un multiple de π, sauf dans le cas où ab=1, où elle n’est pas définie.
Quelle est une méthode simple pour démontrer la formule arctan(a) + arctan(b) = arctan((a+b) / (1-ab))?
La méthode la plus simple pour démontrer la formule est de partir de la formule tan(x+y)=tanx+tany / (1−tanx*tany). Ainsi, les deux membres de l’égalité ont la même tangente. Ensuite, il faut voir dans quels intervalles (modulo π) appartiennent arctan(a)+arctan(b) et arctan((a+b)/(1−ab)).



