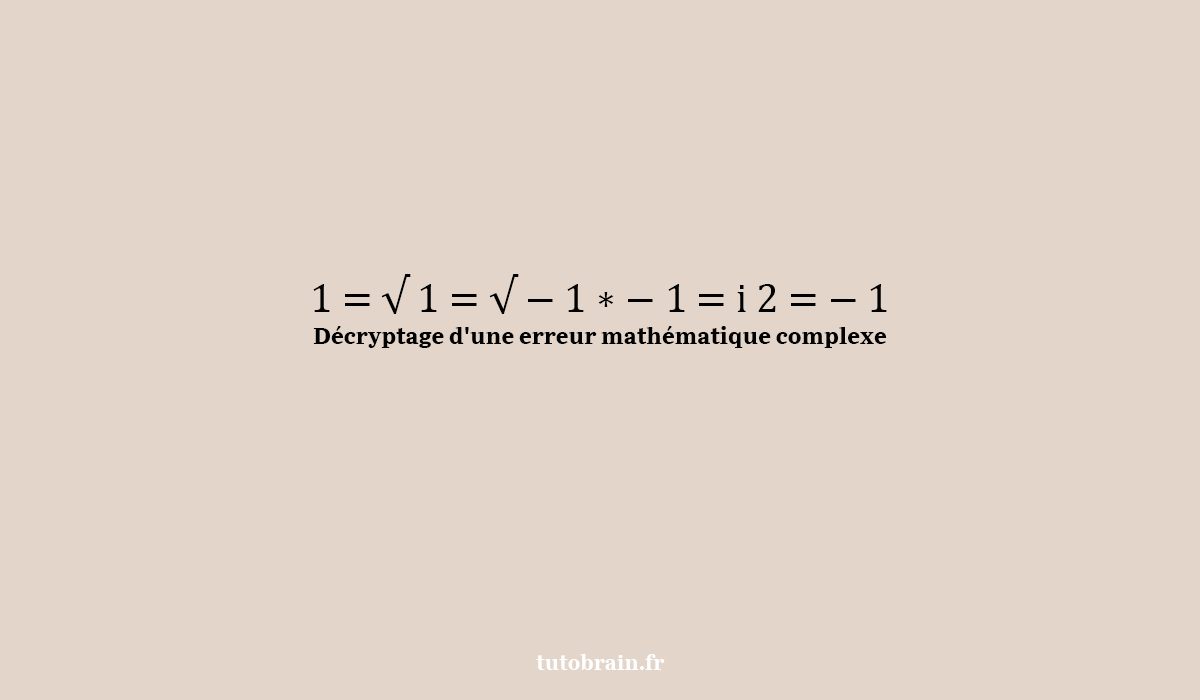Êtes-vous prêt à démystifier une preuve mathématique apparemment infaillible ? Découvrons ensemble ce qui cloche avec la démonstration suivante : 1 = √ 1 = √ − 1 ∗ − 1 = i 2 = − 1. Accrochez-vous, car nous allons plonger dans les méandres des nombres réels et complexes pour dénouer cette énigme mathématique complexe. Préparez-vous à découvrir les implications de cette erreur et à repartir avec des astuces pour éviter de telles embûches en mathématiques. Allons-y !
Au sommaire :
- La preuve mathématique 1 = √ 1 = √ − 1 ∗ − 1 = i 2 = − 1 est fausse car elle ne respecte pas les règles mathématiques de manière cohérente.
- Les ensembles mathématiques Z et Q sont définis comme l’ensemble des nombres entiers relatifs et l’ensemble des nombres rationnels respectivement.
- Il est important de justifier les réponses en mathématiques, par exemple en répondant par vrai ou faux et en expliquant la justification.
- L’écriture en extension des ensembles, comme A={nombres entiers compris entre √2 et 2π}, est une pratique courante en mathématiques.
- La théorie mathématique et les preuves doivent respecter les règles et les théorèmes établis pour être valides.
- Les différents types de raisonnement en mathématiques, tels que le raisonnement par l’absurde, sont utilisés pour démontrer des propositions mathématiques.
Comprendre l’erreur dans une preuve mathématique complexe
La preuve mathématique présentée comme 1 = √1 = √(−1 * −1) = i² = −1 soulève des questions fondamentales sur la manipulation des nombres réels et complexes. Analysons où le raisonnement échoue et pourquoi il est crucial de comprendre les domaines d’application des différentes opérations mathématiques.
La première équivalence 1 = √1 est correcte car la racine carrée de 1 est bien 1. Cependant, les problèmes commencent avec la deuxième équivalence. Bien que mathématiquement correct que (−1) * (−1) = 1, l’erreur provient de l’assimilation de √(−1 * −1) avec i². En réalité, l’opération de racine carrée dans les nombres complexes n’est pas aussi directe que dans les nombres réels et nécessite une approche spécifique.
En introduisant le nombre complexe i, qui est défini par i² = -1, il est essentiel de comprendre que le domaine des nombres réels et celui des nombres complexes fonctionnent différemment. La racine carrée dans les complexes, en particulier, doit être traitée avec prudence car elle peut avoir plusieurs valeurs. Cela nous conduit à l’erreur fondamentale de la preuve : l’assimilation incorrecte des valeurs sans considérer leur contexte spécifique.
Les implications de l’erreur dans les domaines réels et complexes
Par cette preuve, nous observons comment une compréhension incomplète des propriétés des nombres complexes peut conduire à des contradictions apparentes. La racine carrée d’un nombre positif dans les réels est univoque, mais dans les complexes, elle est multivaluée, comme mentionné dans l’analyse des preuves.
Le passage de √1 à √(−1 * −1) est mathématiquement viable, mais l’association de √(−1 * −1) à i² est incorrecte car elle néglige le fait que la racine carrée de 1 peut être à la fois 1 et -1 dans le contexte des nombres complexes. Cette dualité est souvent source de confusion et doit être traitée avec une compréhension claire des principes des nombres complexes.
Cette erreur met en lumière l’importance de la définition correcte des fonctions et de leur domaine de définition. Dans les nombres complexes, où il n’y a pas d’ordre naturel comme dans les réels, les opérations de base peuvent avoir des résultats contre-intuitifs sans une manipulation soigneuse.
Conclusions et meilleures pratiques en mathématiques
La preuve erronée que nous avons examinée est un excellent exemple de l’importance d’une rigueur mathématique. Elle nous enseigne que chaque étape dans une preuve mathématique doit être justifiée clairement et correctement, en tenant compte du domaine des nombres impliqués et des propriétés uniques des opérations comme la racine carrée dans les complexes.
Il est crucial, surtout en mathématiques avancées, de ne pas faire d’hypothèses non vérifiées ou de simplifications excessives qui pourraient conduire à des conclusions incorrectes. Cela est particulièrement vrai dans l’étude des nombres complexes, où les intuitions basées sur les nombres réels peuvent souvent induire en erreur.
Enfin, cette discussion met en évidence la nécessité d’utiliser des définitions précises et d’approcher les problèmes mathématiques avec une compréhension approfondie des théories sous-jacentes. Seules une étude rigoureuse et une pratique attentive des mathématiques peuvent éviter de telles erreurs et développer une compréhension plus profonde des structures numériques complexes comme les nombres complexes.
Ainsi tout étudiant ou professionnel des mathématiques devrait prendre cette erreur comme un rappel de l’importance de la précision et de la clarté dans toutes les démonstrations mathématiques, ainsi que de l’importance de bien comprendre les propriétés fondamentales des opérations et des nombres avec lesquels ils travaillent.
Qu’est-ce qui est faux avec la preuve mathématique suivante: 1 = √ 1 = √ − 1 ∗ − 1 = i 2 = − 1 ?
La conclusion est fausse; le raisonnement est invalide.
Quelles sont les étapes correctes de la preuve mathématique ?
La première équivalence 1 = √1 est correcte car la racine carrée de 1 est bien 1. Ensuite, l’équivalence √1 = √(−1 * −1) est également correcte car le produit de deux réels négatifs est un réel positif. Cependant, l’association de √(−1 * −1) à i² est incorrecte car elle néglige le fait que la racine carrée de 1 peut avoir plusieurs valeurs dans les nombres complexes.
Pourquoi l’association de √(−1 * −1) à i² est-elle incorrecte ?
L’erreur provient de l’assimilation incorrecte des valeurs sans considérer leur contexte spécifique. La racine carrée dans les nombres complexes n’est pas aussi directe que dans les nombres réels et nécessite une approche spécifique. De plus, la racine carrée dans les complexes est multivaluée, ce qui rend l’association avec i² invalide.
Quelle leçon importante peut-on tirer de cette preuve mathématique ?
L’expression “√(-1)” est gravement fautive, autant dans les réels que dans les complexes. Il est essentiel de comprendre que le domaine des nombres réels et celui des nombres complexes fonctionnent différemment, en particulier en ce qui concerne la racine carrée. Il est crucial de considérer le contexte spécifique et les domaines d’application des différentes opérations mathématiques.