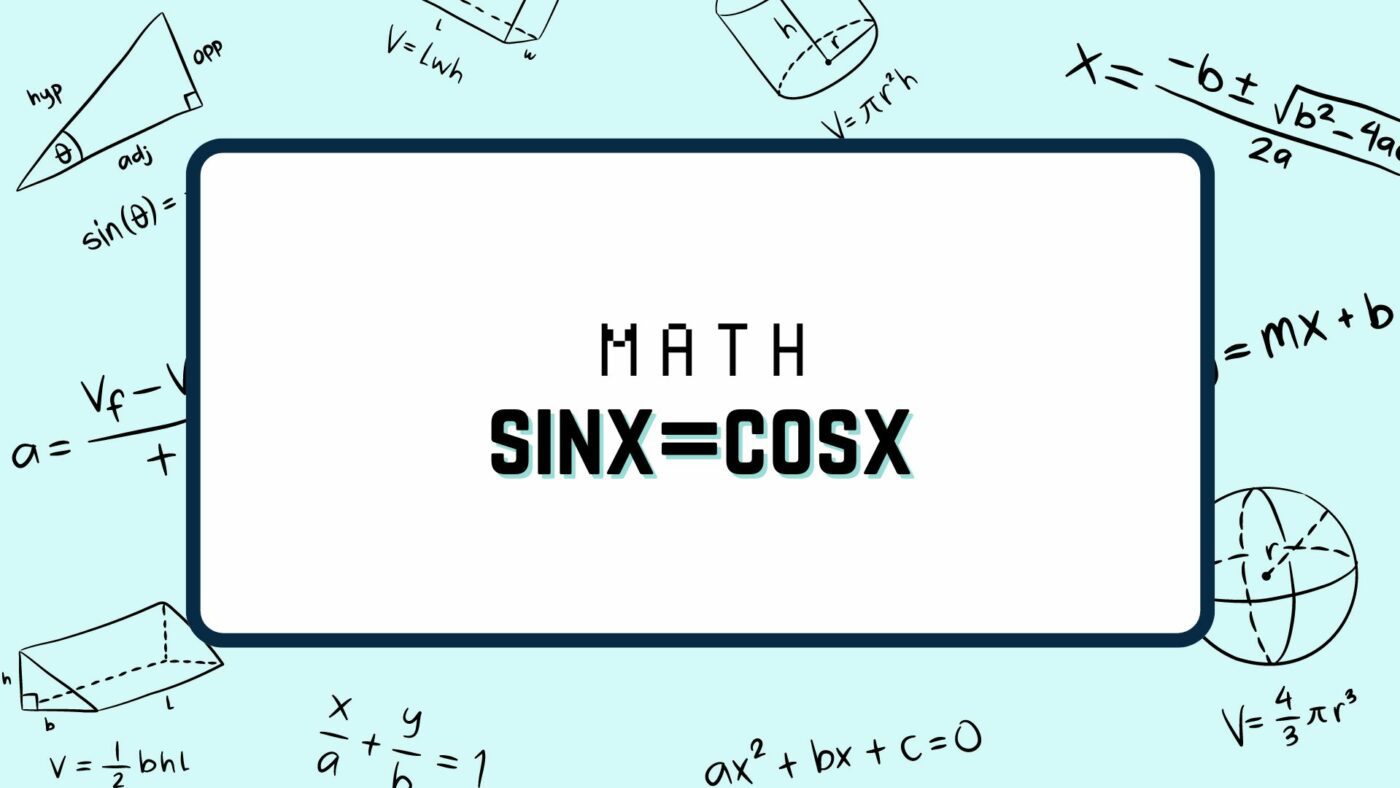Vous vous êtes déjà demandé quelles sont les solutions de l’équation sinx=cosx ? Ne cherchez pas plus loin, car nous allons plonger dans cette énigme mathématique ensemble ! Dans cet article, nous allons explorer l’équation sinx = cosx, comprendre son fonctionnement, et découvrir les solutions de manière simple et efficace. Préparez-vous à démystifier cette équation et à en apprendre davantage sur ses applications pratiques. Accrochez-vous, car nous allons résoudre ce casse-tête mathématique ensemble !
Au sommaire :
- La solution de sin x = cos x se trouve sur la première bissectrice des axes qui coupe le cercle aux points π/4 et −3π/4.
- Changer le symbole d’inégalité par un symbole d’égalité pour résoudre une équation sinus.
- Isoler le rapport sinus pour résoudre une équation sinus.
- La valeur de cos x pour des angles remarquables peut être trouvée dans un tableau de valeurs remarquables.
- Transformer une équation avec une égalité entre deux cosinus en remplaçant le sinus.
- Déplacer la fonction cosx de π/2 unité vers la droite pour obtenir la fonction sinx.
Comprendre l’équation sinx = cosx
L’équation sinx = cosx peut sembler simple à première vue, mais elle renferme des subtilités qui méritent une exploration approfondie. Cette équation trigonométrique est cruciale pour comprendre le comportement des fonctions sinus et cosinus, notamment leur intersection et leur périodicité sur le cercle unité.
Dans le cercle trigonométrique, les points où les valeurs de sinus et de cosinus sont égales sont particulièrement intéressants. Ces points correspondent aux angles où les deux fonctions se rencontrent sur le cercle unité. Mathématiquement, cela se produit aux angles π/4 et -3π/4, ce qui représente visuellement une diagonale du cercle unité.
Il est également important de noter que ces solutions sont périodiques avec une période de π. Cela signifie que pour chaque intervalle de π, le sinus et le cosinus auront les mêmes valeurs à des points correspondants.
L’équation sinx = cosx est donc fondamentale non seulement pour l’étude de la trigonométrie, mais aussi pour de nombreuses applications en physique et en ingénierie où les phénomènes périodiques sont courants.
Approche mathématique et résolution
Pour résoudre l’équation sinx = cosx, une méthode consiste à utiliser les propriétés des fonctions trigonométriques. En trigonométrie, il est bien connu que sinx = cos(π/2 – x). Ainsi, résoudre sinx = cosx revient à résoudre x = π/2 – x. Cela conduit à x = π/4 ou x = -3π/4 comme mentionné précédemment.
En approfondissant avec les calculs fournis, on peut voir que l’équation est transformée en une équation du second degré après certains manipulations algébriques et trigonométriques. Avec les valeurs de sin(2x) trouvées, on peut déduire les valeurs correspondantes de x en utilisant la fonction arcsin, suivi d’une division par 2 pour ajuster l’angle. Cela conduit à des formules générales pour toutes les solutions possibles en tenant compte de la périodicité.
Il est crucial de vérifier que les solutions satisfassent l’équation initiale, car l’élévation au carré des deux membres d’une équation peut introduire des solutions extrinsèques. Cela garantit que les solutions trouvées sont non seulement mathématiquement correctes mais aussi applicables à l’équation originale.
Applications pratiques et conclusion
L’équation sinx = cosx et ses solutions ne se limitent pas uniquement à des problèmes académiques. Elles trouvent des applications dans des domaines variés tels que la conception d’ondes et signaux en ingénierie électrique, l’analyse de mouvements périodiques en physique, et même dans des algorithmes de cryptographie basés sur des propriétés trigonométriques.
Comprendre où et comment les fonctions sinus et cosinus se rencontrent sur le cercle unité peut aider à modéliser et à prévoir le comportement de systèmes oscillants et rotatifs, ce qui est essentiel dans la conception de moteurs et de capteurs.
En conclusion, l’étude de l’équation sinx = cosx révèle des principes fondamentaux de la trigonométrie tout en ouvrant la porte à des applications pratiques diverses. Elle illustre parfaitement comment une formule mathématique apparemment simple peut avoir des implications profondes et larges.
Quelles sont les points d’intersection des fonctions sinus et cosinus sur le cercle unité ?
Les points d’intersection des fonctions sinus et cosinus sur le cercle unité correspondent aux angles π/4 et -3π/4.
Quelles sont les solutions périodiques de l’équation sinx=cosx ?
Les solutions périodiques de l’équation sinx=cosx sont x = π/4 + kπ et x = -3π/4 + kπ, où k est un entier relatif.
Quelle méthode mathématique peut-on utiliser pour résoudre l’équation sinx=cosx ?
Une méthode consiste à utiliser les propriétés des fonctions trigonométriques, telles que sinx = cos(π/2 – x), pour résoudre l’équation.